问题描述

---

思路分析：

问题分析：

小E需要计算射击点 (x, y) 的得分，得分依据点到靶心 (0, 0) 的距离决定：

1. 靶心内（半径为 1）得 10 分；
2. 每向外扩展一环（半径为 2、3…10），得分递减 1 分；
3. 超过所有环（半径大于 10）得 0 分。

关键是判断射击点位于哪个环，依次计算得分。

解题思路：

1. 数学分析：

• 点到原点的距离公式为：
  

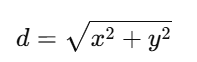
• 判断点是否位于第 i 个环内，只需判断：d ≤ i
• 使用距离平方代替平方根计算，避免浮点运算，提高性能：d² = x² + y² 与 i² 比较

1. 逐环判断：

• 从第 1 个环开始，依次检查点 (x, y) 是否满足条件 d² ≤ i² ；
• 找到满足条件的最小 i ，其对应得分为 11 – i 。

1. 超出所有环：

• 如果点的距离平方 d² > 100（即 10² ），则不在任何环内，得分为 0 。

算法实现步骤：

1. 计算距离平方：

• 使用公式 x² + y² 得到距离平方。

1. 逐环遍历：

• 用一个循环从 i = 1 到 i = 10 ，依次判断距离平方是否小于等于 i² 。

1. 返回得分：

• 如果找到对应的 i ，返回 11 – i ；
• 如果循环结束，返回 0 分。

复杂度分析：

1. 时间复杂度：

• 最多需要遍历 10 次，时间复杂度为 O(1) 。

1. 空间复杂度：

• 只需存储若干变量，空间复杂度为 O(1) 。

---

参考代码（Java）

public class Main {
    public static int solution(int x, int y) {
        // 计算点 (x, y) 到原点 (0, 0) 的距离平方
        int distanceSquared = x * x + y * y;

        // 判断射击点在哪个环内
        for (int i = 1; i <= 10; i++) {
            if (distanceSquared <= i * i) {
                return 11 - i; // 得分公式
            }
        }

        // 如果超出所有环，得0分
        return 0;
    }

    public static void main(String[] args) {
        System.out.println(solution(1, 0) == 10); 
        System.out.println(solution(1, 1) == 9); 
        System.out.println(solution(0, 5) == 6); 
        System.out.println(solution(3, 4) == 6); 
    }
}

代码分析

1. int distanceSquared = x * x + y * y;

• 目的：计算点 (x, y) 到原点 (0, 0) 的距离平方。
• 原理：使用公式 x² + y² ，避免调用 Math.sqrt 减少浮点运算，提高性能。

2. for (int i = 1; i <= 10; i++)

• 目的：依次判断点 (x, y) 所处的环。
• 逻辑：
• 环的半径依次为 1, 2, 3, …… , 10 ，半径平方为 1², 2², 3², ….., 10² 。
• 若 distanceSquared <= i * i，说明点在当前半径 i 所对应的环内。

3. if (distanceSquared <= i * i)

• 判断条件：
• 比较点的距离平方 distanceSquared 和当前环的半径平方 i² 。
• 满足条件则返回得分，得分公式为 11 – i 。

4. return 11 - i;

• 得分公式：对于第 i 个环，得分为 11 – i ：
• 靶心（第 1 环）：得分 11 – 1 = 10 ；
• 第 2 环：得分 11 – 2 = 9 ；
• …
• 第 10 环：得分 11 – 10 = 1 。

5. return 0;

• 处理超出范围：
• 若点的距离平方 d² > 100（即 10² ） ，说明点不在任何环内；
• 返回 0 分。

改进建议：
如果环的数量大幅增加，可以考虑二分查找优化判断逻辑，将复杂度降为 O(logn) 。