一、 哈希查找的基本原理
哈希查找的核心思想是通过一个哈希函数将关键字快速映射到存储空间的位置,从而实现高效的查找操作。
1. 哈希函数的定义
哈希函数是一个数学函数,用来将任意大小的输入映射到有限的地址空间。例如:
h(key) = key % m
- key :要存储或查找的关键字。
- m :哈希表的大小。
2. 哈希表的特点
- 直接寻址:通过哈希函数,直接计算关键字在表中的存储位置。
- 高效查找:查找时间复杂度接近 O(1) (理想情况)。
- 冲突问题:由于不同关键字可能映射到同一个位置(称为哈希冲突),需要解决冲突。
二、 哈希查找填表的具体步骤
假设我们需要插入以下关键字:10、20、5、15、35、17,哈希表大小为 m = 7 ,采用以下设置:
- 哈希函数:h(key) = key % m 。
- 冲突解决方法:线性探测法(冲突时依次寻找下一个空位)。
1. 初始化哈希表
创建一个长度为 7 的数组,初始时每个位置为空:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
2. 插入关键字
每个关键字的操作如下:
- 插入 10:
- 计算哈希值: h(10) = 10 % 7 = 3 。
- 将 10 存储在索引 3:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 10 |
- 插入 20:
- 计算哈希值: h(20) = 20 % 7 = 6 。
- 将 20 存储在索引 6:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 10 | 20 |
- 插入 5:
- 计算哈希值: h(5) = 5 % 7 = 5 。
- 将 5 存储在索引 5:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 10 | 5 | 20 |
- 插入 15:
- 计算哈希值: h(15) = 15 % 7 = 1 。
- 将 15 存储在索引 1:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 15 | 10 | 5 | 20 |
- 插入 35:
- 计算哈希值: h(35) = 35 % 7 = 0 。
- 将 35 存储在索引 0:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 35 | 15 | 10 | 5 | 20 |
- 插入 17:
- 计算哈希值: h(17) = 17 % 7 = 3 。
- 发现索引 3 已经存储了 10 ,发生冲突。
- 使用线性探测法,依次检查下一个空位:
- 索引 4 为空,将 17 存入:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 35 | 15 | 10 | 17 | 5 | 20 |
三、 冲突的解决方法详解
冲突是哈希表操作中不可避免的问题。下面讲解几种常用的冲突解决方法,如何影响填表过程。
1. 开放地址法
开放地址法的核心思想是:当哈希函数计算出的地址已被占用时,通过一定的规则寻找其他空闲位置。
常见方法:
- 线性探测:
- 每次探测相邻的下一个位置,直到找到空位。
- 如果索引 i 冲突,尝试位置: i+1, i+2, … , i+m-1 (对表大小m取模)
- 二次探测:
- 避免线性探测导致的“堆积”问题。
- 探测位置: i+12, i-12, i+22, i+22 , …
2. 链地址法
链地址法的核心思想是:每个哈希表位置存储一个链表,所有冲突的数据都存放在链表中。
- 插入:将冲突的数据插入链表尾部或头部。
- 查找:在链表中查找目标值。
示例:
假设关键字 10 和 17 冲突,使用链地址法时:
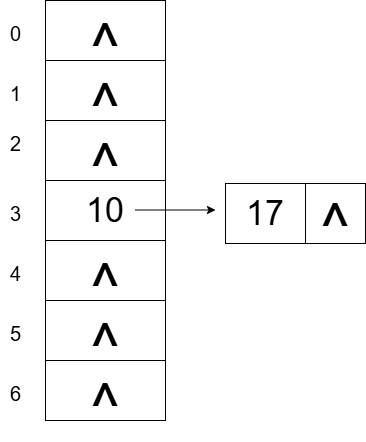
四、 计算平均查找长度
公式
根据冲突处理方法,平均查找长度的公式如下:

例题讲解
链地址法成功查找的平均查找长度
假设哈希表大小 m = 10 ,关键字个数 n = 20 ,每条链表存储的关键字个数如下:
$[2, 3, 0, 4, 1, 5, 2, 1, 2, 0]$
步骤 1:计算每条链表的查找长度
- 链表长度查找平均值为链表长度的一半。例如,链表长度为 4,其平均查找长度为
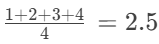
步骤 2:总查找长度
- 总查找长度为每条链表的关键字数 $\times$ 平均查找次数。
- 对每个链表计算:
- 索引 0: 2 × 1.5 = 3
- 索引 1: 3 × 2 = 6
- 索引 3: 4 × 2.5 = 10
- 索引 4: 1 × 1 = 1
- 索引 5: 5 × 3 = 15
- 索引 6: 2 × 1.5 = 3
- 索引 7: 1 × 1 = 1
- 索引 8: 2 × 1.5 = 3
步骤 3:计算平均查找长度
总查找长度为:
3 + 6 + 10 + 1 + 15 + 3 + 1 + 3 = 42
关键字总数为 n = 20 ,因此:
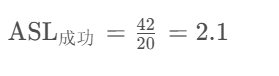
评论留言
欢迎您,!您可以在这里畅言您的的观点与见解!
0 条评论
