利用栈完成拓扑排序的基本思想是通过入度（in-degree）记录每个顶点的依赖关系，依次处理入度为0的顶点，并更新其他顶点的入度，直到所有顶点都被处理。

---

计算方法

1. 构建入度数组：
   • 通过遍历邻接表，统计每个顶点的入度，并存储在数组中。
2. 初始化栈：
   • 将所有入度为0的顶点入栈，因为它们不依赖于其他顶点。
3. 处理栈：

• 重复以下步骤，直到栈为空：
  1. 从栈中取出一个顶点，记录为拓扑排序结果。
  2. 遍历该顶点的邻接表，对其所有邻接点的入度减1。
  3. 如果某个邻接点的入度减为0，则将该顶点入栈。

• 检查结果：
  • 如果处理完所有顶点且拓扑排序结果包含所有顶点，则成功；否则说明图中存在环，不是有向无环图（DAG）。

---

举例分析

例1

我们有以下有向图，其邻接表表示如下：

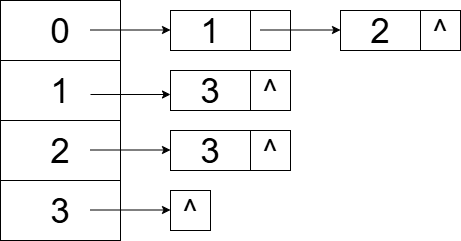
步骤1：计算所有顶点的入度

1. 遍历邻接表：
   • 顶点 0 没有任何入边，入度为 0。
   • 顶点 1 被顶点 0 指向，入度为 1。
   • 顶点 2 被顶点 0 指向，入度为 1。
   • 顶点 3 被顶点 1 和 2 指向，入度为 2。

入度结果：

入度数组：0 -> 0, 1 -> 1, 2 -> 1, 3 -> 2

步骤2：将入度为0的顶点入栈

1. 检查每个顶点的入度：
   • 顶点 0 入度为 0，因此将 0 入栈。

初始栈：

栈： [0]

步骤3：开始处理栈中的顶点，逐步更新入度

我们依次弹出栈顶顶点，更新其邻接点的入度。邻接点的入度每次减少1，当入度变为0时将其入栈。

第1次处理栈：

• 弹出顶点 0。
• 将 0 记录为拓扑排序的第一个顶点。
• 遍历顶点 0 的邻接点 1 和 2：
• 顶点 1 的入度由 1 减为 0，将 1 入栈。
• 顶点 2 的入度由 1 减为 0，将 2 入栈。

结果：

拓扑序列： [0]
栈： [1, 2]
入度更新：0 -> 0, 1 -> 0, 2 -> 0, 3 -> 2

第2次处理栈：

• 弹出顶点 2。
• 将 2 记录为拓扑排序的第二个顶点。
• 遍历顶点 2 的邻接点 3：
• 顶点 3 的入度由 2 减为 1（尚未达到0）。

结果：

拓扑序列： [0, 2]
栈： [1]
入度更新：0 -> 0, 1 -> 0, 2 -> 0, 3 -> 1

第3次处理栈：

• 弹出顶点 1。
• 将 1 记录为拓扑排序的第三个顶点。
• 遍历顶点 1 的邻接点 3：
• 顶点 3 的入度由 1 减为 0，将 3 入栈。

结果：

拓扑序列： [0, 2, 1]
栈： [3]
入度更新：0 -> 0, 1 -> 0, 2 -> 0, 3 -> 0

第4次处理栈：

• 弹出顶点 3。
• 将 3 记录为拓扑排序的第四个顶点。
• 顶点 3 没有邻接点，因此无需更新其他顶点的入度。

结果：

拓扑序列： [0, 2, 1, 3]
栈： []
入度更新：0 -> 0, 1 -> 0, 2 -> 0, 3 -> 0

步骤4：检查是否所有顶点被处理

1. 栈为空，表示所有顶点都已被处理。
2. 拓扑排序完成，得到的序列 [0, 2, 1, 3] 是一个有效的拓扑排序。

各顶点的入栈情况

• 顶点 0：在初始扫描时入栈。
• 顶点 1：在处理顶点 0 时，入度减为0后入栈。
• 顶点 2：在处理顶点 0 时，入度减为0后入栈。
• 顶点 3：在处理顶点 1 时，入度减为0后入栈。

拓扑排序逻辑总结

1. 初始扫描图中所有顶点，将入度为0的顶点入栈。
2. 每次弹出栈顶顶点，记录为拓扑序列中的一个顶点。
3. 更新邻接点的入度，任何入度变为0的顶点立即入栈。
4. 循环处理，直到栈为空。如果最后处理的顶点数少于图的顶点数，说明图中存在环。

最终拓扑排序结果为：

[0, 2, 1, 3]

当然也可以为：

[0, 1, 2, 3] 

---

例2

我们有以下有向图，其邻接表表示如下：

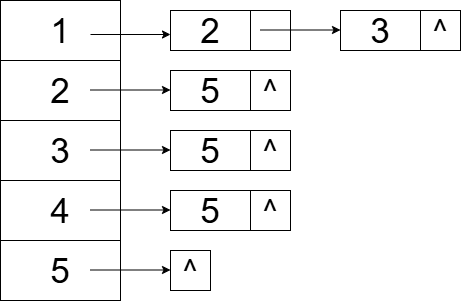
步骤1：计算各顶点的入度

遍历邻接表，统计每个顶点的入度：

• 顶点 1：没有入边，入度为 0。
• 顶点 2：被顶点 1 指向，入度为 1。
• 顶点 3：被顶点 1 指向，入度为 1。
• 顶点 4：没有入边，入度为 0。
• 顶点 5：被顶点 2、3、4 指向，入度为 3。

入度数组：

入度：1 -> 0, 2 -> 1, 3 -> 1, 4 -> 0, 5 -> 3

步骤2：初始入栈

1. 找到所有入度为 0 的顶点，将它们入栈：
   • 顶点 1 和顶点 4 入栈。
   • 初始栈：[1, 4]

步骤3：处理栈中顶点

开始弹出栈顶顶点，并更新邻接点的入度。如果某个邻接点的入度变为 0，将其入栈。

第1次处理栈

• 弹出顶点 4，记录为拓扑序列的第一个顶点。
• 顶点 4 的邻接点是 5：
  • 顶点 5 的入度从 3 减为 2（尚未达到 0）。
• 栈：[1]
• 拓扑序列：[4]

第2次处理栈

• 弹出顶点 1，记录为拓扑序列的第二个顶点。
• 顶点 1 的邻接点是 2 和 3：
  • 顶点 2 的入度从 1 减为 0，将 2 入栈。
  • 顶点 3 的入度从 1 减为 0，将 3 入栈。
• 栈：[2, 3]
• 拓扑序列：[4, 1]

第3次处理栈

• 弹出顶点 3，记录为拓扑序列的第三个顶点。
• 顶点 3 的邻接点是 5：
  • 顶点 5 的入度从 2 减为 1（尚未达到 0）。
• 栈：[2]
• 拓扑序列：[4, 1, 3]

第4次处理栈

• 弹出顶点 2，记录为拓扑序列的第四个顶点。
• 顶点 2 的邻接点是 5：
  • 顶点 5 的入度从 1 减为 0，将 5 入栈。
• 栈：[5]
• 拓扑序列：[4, 1, 3, 2]

第5次处理栈

• 弹出顶点 5，记录为拓扑序列的第五个顶点。
• 顶点 5 没有邻接点，无需更新。
• 栈：[]
• 拓扑序列：[4, 1, 3, 2, 5]

结果

• 入栈顺序（按照入栈时间记录）：

1. 初始入栈：[1, 4]
2. 处理顶点 1 时，2 和 3 入栈。
3. 处理顶点 2 和 3 时，5 入栈。

• 完整入栈情况：[1, 4, 2, 3, 5]
• 拓扑排序次序（出栈顺序）
  • 拓扑序列：[4, 1, 3, 2, 5]

注意：拓扑排序的多种可能性

拓扑排序可能有多种结果，取决于同时满足入度为 0 的顶点在栈中的处理顺序。例如：

• 如果优先处理顶点 1 后再处理顶点 4，结果可能是：[1, 4, 2, 3, 5]。
• 当前结果 [4, 1, 3, 2, 5] 依然是一个有效的拓扑排序。